Built 2025-10-01T20:43:04.267910Z — TRM v1.2a (Dream → Design → Verify → Expand; tone: prosecutorial; scope +100)
The Hidden Highways of Space: Gravity‑Assists & Lagrange Points for Builders
We will put orbital “highways” in the hands of ordinary builders. Not by rationing access to knowledge or treating mission design like priestcraft, but by publishing maps and methods that let a motivated teen, a teacher, a maker club, and a small shop think and talk like mission designers. We honor real physics and hard limits; we refuse the story that progress belongs only to approved labs or monopolies. We open the gate for those with limited budgets and large ambitions.
1. Opening case (prosecutorial)
If access to space depends only on brute propellant and closed capital, newcomers stay out. The physics already offers leverage: trade momentum with a moving planet (a gravity‑assist) and use balance regions in the Sun–Earth system (Lagrange points). These two ideas — momentum trades and balance zones — form practical “space highways”. The maps exist in technical literature and mission archives; what’s been missing is translation into low‑cost tools and demos for lower‑income entrants. That is the focus of this piece.
2. Gravity‑assist in plain terms
In the planet’s own frame, you approach and depart with roughly the same speed (ignoring losses). In the Sun’s frame, the planet’s velocity adds vectorially to yours so you can depart faster or slower or on a new heading without paying that change in fuel. You are borrowing a hair of the planet’s orbital momentum. The planet’s change is imperceptible; your win is decisive. A well‑timed burn at the closest point of approach (the Oberth effect) multiplies the energy gained per unit of propellant.
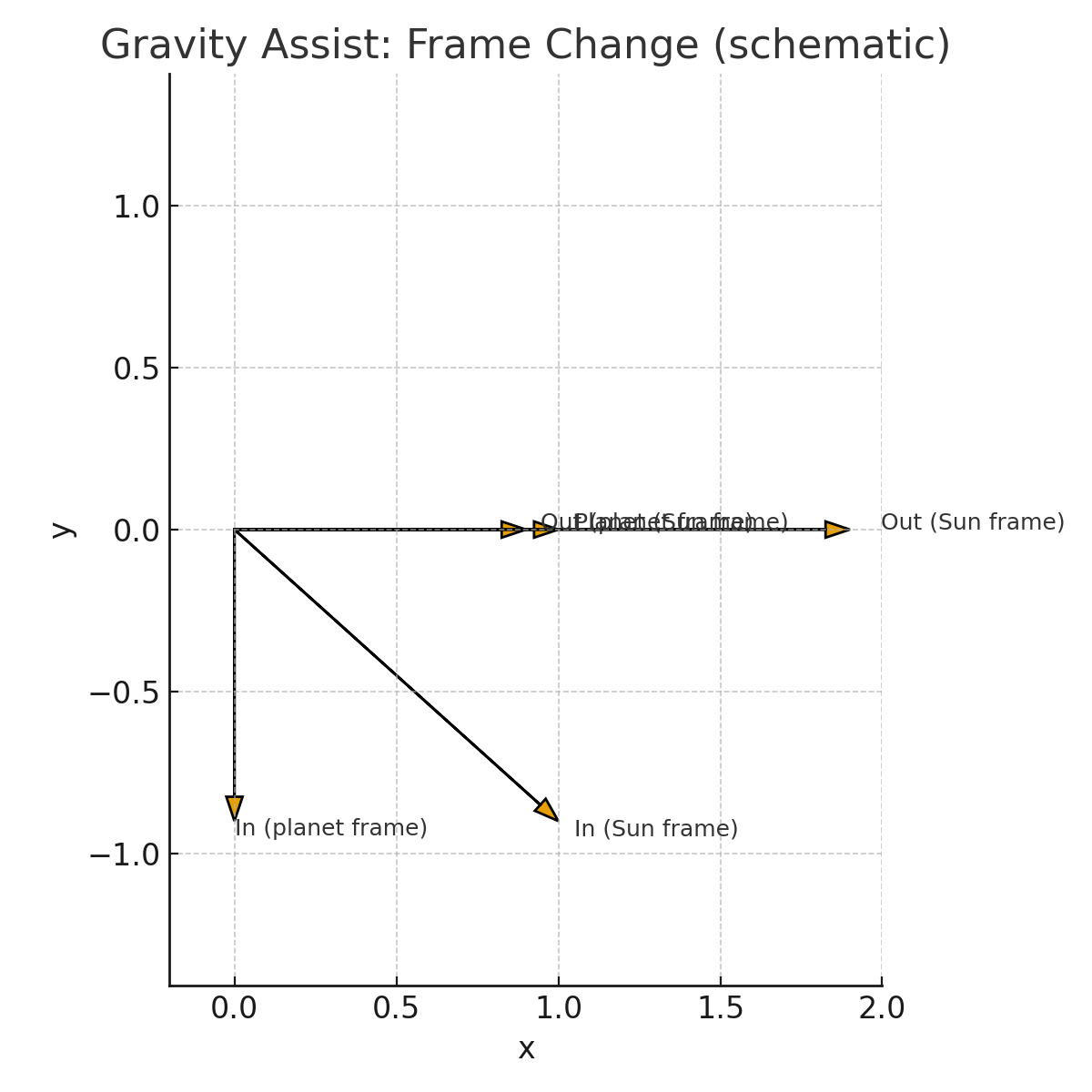
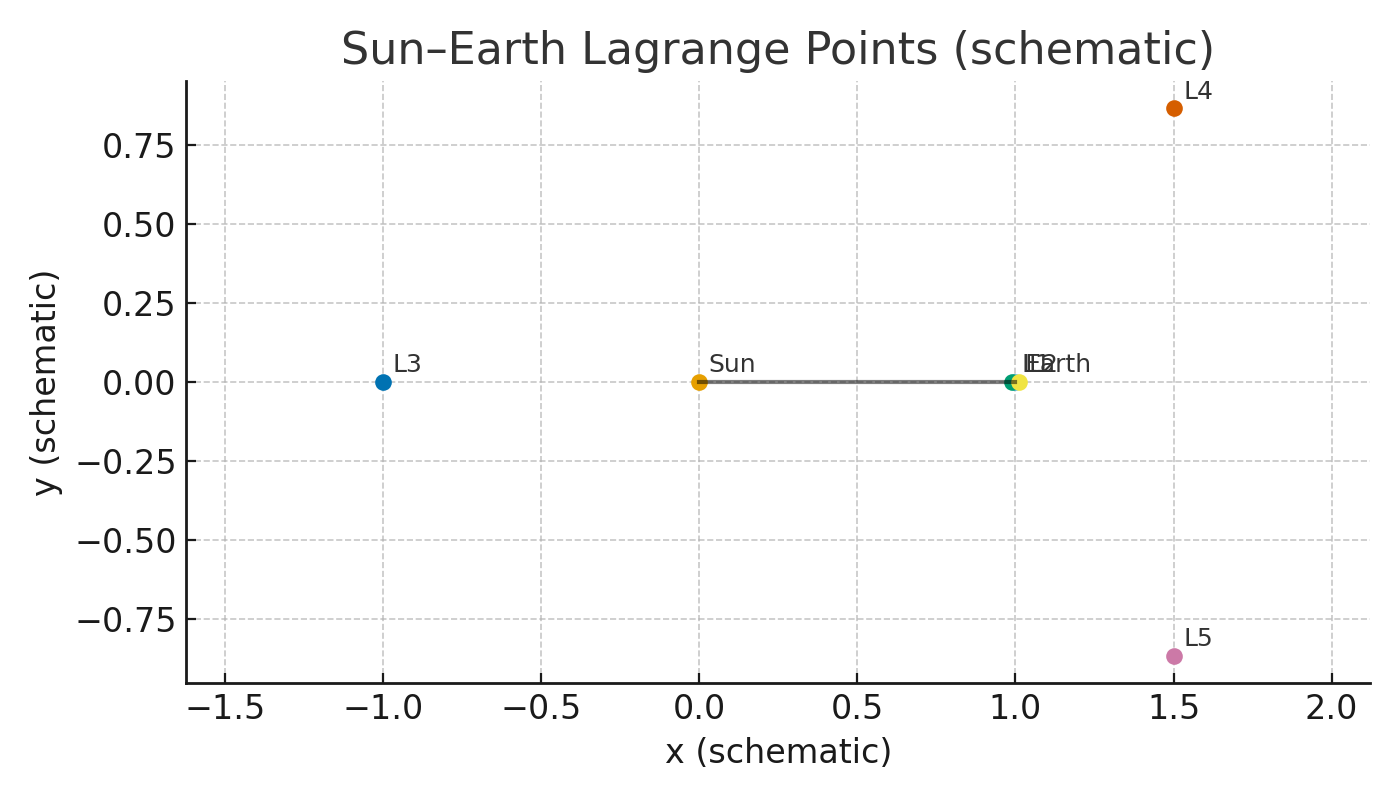
3. Lagrange points in one picture
In the Sun–Earth system there are five positions where a small object can stay in step with Earth’s year: L1 through L5. L1 sits between Sun and Earth; L2 sits beyond Earth; L3 is opposite Earth across the Sun; L4 and L5 form the third corners of equilateral triangles with Sun and Earth. Spacecraft don’t sit exactly on L1/L2/L3; they orbit nearby in “halo” or “Lissajous” loops with modest station‑keeping. L4/L5 can be stable islands when the mass ratio is favorable. The James Webb Space Telescope operates near Sun–Earth L2, roughly 930,000 miles from Earth.
4. Highways, not straight lines
By chaining flybys and L‑point halos, designers create long‑reach routes that sip propellant. Low‑energy pathways such as the weak‑stability boundary can act as gentle on‑ramps to far targets. These are delicate to plan but open doors for small missions that would otherwise be priced out.
5. Three plays explained like road trips
- Voyager Grand Tour — a Jupiter slingshot bent the path to Saturn; Voyager 2 continued to Uranus and Neptune.
- Cassini (V‑V‑E‑J‑G‑A) — a chain of assists (two Venus flybys, then Earth, then Jupiter) that made Saturn capture affordable.
- JWST at L2 — a large sunshield only works if Sun, Earth, and Moon stay on the same side; a halo orbit near L2 keeps the telescope cold and in contact.
6. Build it at home
Marble slingshot: a rotating “planet” (lazy susan) and marbles. Aim to skim the hub and watch exit speed/heading change with pass geometry. Balance‑point beam: two magnets and a steel ball along a ruler. Find the spots where forces balance but small nudges drift — saddle intuition.
7. Read a mission page like a pro
Check the reference frame used for arrows; look for closest‑approach burns (Oberth); identify halo segments around L1/L2.
8. What this makes possible
L2 for everyone (weather, astronomy, relays). Tiny missions with long reach (schools, clubs, startups). A literate public that can read trajectories and write basic “briefs” the way people once learned to read maps.
Units: Imperial only. Distances are given in miles; diagrams are schematic with no metric labels.